- Die Graviationskraft einer (homogenen) Kugel, entspricht der Gravitationskraft ihrer Masse im Schwerpunkt konzentriert - ausserhalb der Kugel
- äquivalent gilt das für eine Sphäre (Kugelschale) (innerhalb der Sphäre 0)
- Die Massenverteilung in einer Kugel muss also nicht homogen sein, sondern lediglich ein Funktion vom Abstand zum Zentrum.
- das gilt nicht für Körper anderer Formen, wir fallen ja auch Richtung des Schwerpunkts der Erde und nicht des Sonnensystems.
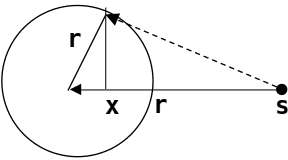
Sphäre mit Radius r - homogen mit Masse belegt, Gravitationsbeschleunigung in einem Punkt im Abstand s von Mittelpunkt.
- Wir ignorieren konstante Faktoren wie das spezifische Gewicht oder die Gravitationskonstante G. Also Kugeloberfläche = Gesamtasse.
- Wir integrieren über die Ringe in einer Ebene senkrecht zur Verbindung Zentrum s, mit Abstand x vom Zentrum
- {`int_{x=-r}^{+r} 2 pi r dx = 4 pi r^2`} = Kugeloberfläche = Gesamtasse
- Abstand-Quadrat von s zu Punkt auf Ring auf Höhe x = {`(s-x)^2 + r^2 - x^2 = s^2 + r^2 -2sx`}
- Graviationsbeschleunigung des Rings bei x auf s = {`2 pi r frac{x - s}{(s^2 + r^2 -2sx)^{3/2}} dx `}
- Graviationsbeschleunigung der ganzen Schale mit Radius r auf s = {`int_{x=-r}^{+r} 2 pi r frac{x - s}{(s^2 + r^2 -2sx)^{3/2}} dx `}
- Integral {`int (ax + b) (cx + d)^eta dx = frac{a c (eta+1) x + b c ( eta + 2 ) - a d}{(eta + 1) (eta + 2) c^2} (cx + d)^{eta+1}`}
- {`int 2 pi r frac{x - s}{(s^2 + r^2 -2sx)^[3/2]} dx = 2 pi r frac{-2s (-1/2 ) x + 2 s^2 ( + 1/2 ) - s^2 - r^2 }[(- 1/2 ) (+ 1/2) 4 s^2 sqrt (s^2 + r^2 -2sx)] = frac{ 2 pi r} { s^2 } frac{ -s x + r ^ 2 } { sqrt (s^2 + r^2 -2sx ) } `}
- {`int_{x=-r}^{+r} ... = frac{ 2 pi r} { s^2 } [ frac{ -s x + r ^ 2 } { sqrt (s^2 + r^2 -2sx ) } ]_{x=-r}^{+r} = frac{ 2 pi r} { s^2 } [ frac{ - s r + r ^ 2 } { sqrt (s^2 + r^2 -2sr ) } - frac{ s r + r ^ 2 } { sqrt (s^2 + r^2 +2sr ) } ] = frac{ 2 pi r^2 } { s^2 } [- frac( s-r )(| s-r |) - frac( s+r )(| s+r |) ] = - frac{ 2 pi r^2 } { s^2 } [ sign( s-r ) + sign( s+r ) ] `} with sign(0) undefined
- also Betrag der Beschleunigung {`= { (frac "MasseDerKugel(schale)" ( "AbstandVonSchwerpunkt"^2 ) G , " if " |s| > |r| ), (0 , " if " |s| < |r| ) :} `}
