Categories: Adjoint Functors

Equivalent definitions of adjoint functors

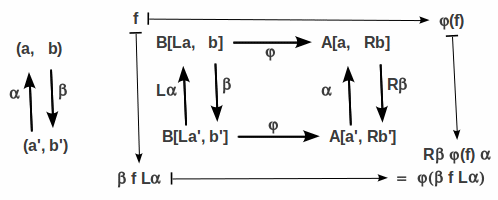1. Given two categories A, B and two functors L: A --> B and R: A <-- B. L is left adjoint to R iff there is a natural isomorphism
   • φ: R[L _, _ ] --> L[ _, R _ ]
   • natural isomorphism means that the φ_a,b build a natural transformation A^op × B --> Set and that each φ_a,b is a bijection
     
2. Given two categories A, B and two functors L: A --> B and R: A <-- B. L is left adjoint to R iff there are natural transformations
   • the unit ε: LR --> 1_B and
   • the counit η: 1_A --> RL
   • with the triangle equations
     • Rε • η_R = 1, i.e. ∀ b ∈ B: Rε_b • η_Rb = 1_b, namely Rb --η_Rb--> RLRb --Rε_b--> Rb and
     • ε_L • Lη = 1, i.e. ∀ a ∈ A: ε_La • Lη_a = 1_a, namely La --Lη_a --> LRLa--ε_La--> La
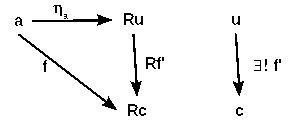3. Given two categories A, B and a functor R: A <-- B and
   • ∀a ∈ A there is an universal arrow η_a: a --> Ru for R,
   • i.e. ∀ f: a --> Rc ∃! f': u --> c with f = η_a • Rf'
4. the dual with a functor L: A --> B and couniversal arrows
   

Proof: 1 ⇒ 2

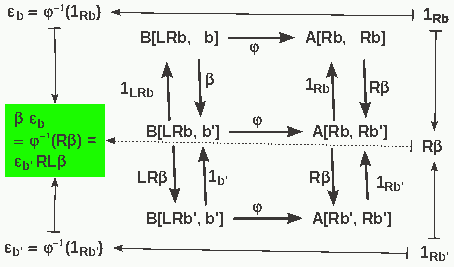1. define ε_b = φ^-1(1_Rb)
2. the diagram shows, that this defines a morphism ε_b: RLb --> b and that it is natural
3. (furhtermore, the equation in the green box shows that φ is defineded by its values on 1, this is the contents of the yoneda lemma)
4. dually η_a = φ(1_La) is a natural transformation
   
5. This diagram prooves one of the dual triangle equations.
   

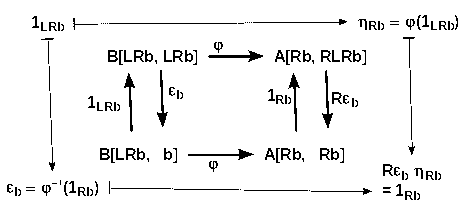
Proof: 2 ⇒ 3

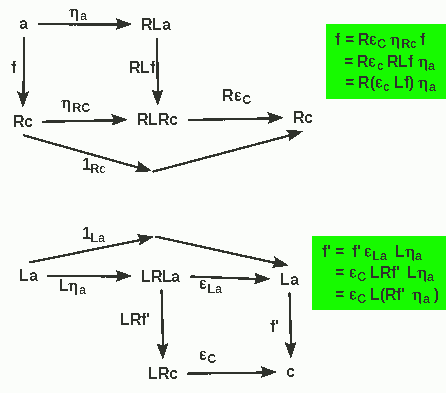1. Given a ∈ A we use a --η_a--> RLa as universal arrow.
2. For any f: a --> Rc we find the required f' = ε_c Lf : La --> c as shown in the upper diagram
3. On the other hand, the lower diagram shows that each such f' can be calculated from Rf' η_a which is nothing but the original f. Thus it is unique.
   

Proof: 3 ⇒ 1

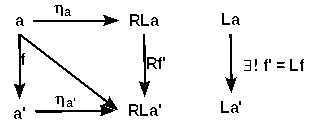1. we construct L as
   • the image La of an object a ∈ A is u from the universal arrow a --> Ru
   • the image Lf of a morphism f: a --> a' is the unique (η_a' f)' of the universal arrow a --η_a--> La for η_a' f
2. we define φ_{a, b}: [La, b] --> [a, Rb] as f' |--> Rf' η_a
   
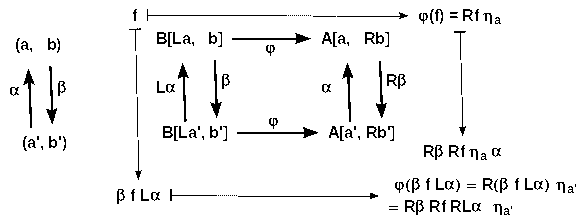3. φ_{a, b} is bijective because of the ∃! in the universal arrow
4. the diagram beside spells out naturality of φ. But by construction of L we have η_a α = RLα η_a'. Thus, the diagram is commuatitve, and hence, φ natural.
5. thus, φ is the required natural isomorphism [L_, _] --> [_, R_] for the adjunction

Proof: ⇐ 4 ⇒

• we omit these proofs because 3 and 4 are dual, left and right adjoint are dual, etc..